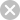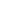Fillable Printable Sample Physics Lab Report
Fillable Printable Sample Physics Lab Report
Sample Physics Lab Report
Guidelines for a Physics Lab Reports
A laboratory report has three main functions:
(1) To provide a record of the experiments and raw data included in the report,
(2) To provide sufficient information to reproduce or extend the data, and
(3) To analyze the data, present conclusions and make recommendations based on the
experimental work.
General Comments:
The single most important requirement for a laboratory report is clarity. Imagine that your
audience is one of your cla ssmate s who missed that experiment.
If you are using a word processor for your lab report, then use the spelling and grammar
checkers. The grammar check can be annoying because often technical sentences are wordy
and complex, but it will help you avoid using too many passive sentences. In general, passive
sentences are less understandable. However, grammar check will not assess clarity, and it will
ignore simple errors. (I do not doubt there are still mistakes in this document I have run it through
spelling and grammar che cks.)
Many technical writers prefer to write sentences with passive verbs. A simple example: “The
spring constant k was found from the slope to be 3.02 N/m.” If you run this sentence through the
grammar check, it will tell you that “was found” is a verb in the passive voice. To change this to
an active voice you could write: “The spring constant k is the slope, 3.02 N/m.” Not every
sentence has to be in an active voice. What you want is a report that is readable.
Lab Report Structure:
I. Cover Sheet: This pa ge has the course number and assigned lab se ction, the title of the
experiment, your name, your lab partner’s names, the date that the lab was performed and
your TA’s name.
II. Abstract: The purpose of an abstract in a scientific paper is to help a reader decide if your
paper is of interest to him/her. (This section is the executive summary in a corporation or
government report; it is often the only section that a manager rea ds.)
The abstract should be able to stand by itself, and
it should be brief. Generally, it consists of
three parts which answer these questio ns:
What did you do? – A statement of the purpose of the experiment, a concise
description of the experiment and physics principl es investigated.
What were your results? – Highlight the most significant results of the experiment.
What do these results tell you? – Depending on the type of experiment, this is
conclusions and implications of the results or it may be lessons learned form the
experiment.
Write the abstract after all the other sections are completed. (You need to know everything in
the report bef ore you can write a summary of it.)
III. Data Sheets: For each experiment, the lab manual has one or more data sheets for
recording raw data, as well as, intermediate and final data values. These are not for doodling,
but for recording your data. Record the data neatly in pen. If your data values are so sloppily
recorded that you have to recopy them, then the accuracy of the data is questionable. This
fact will be reflected in your laboratory performance score. If there is a mistake, then draw a
single line through that value.
“White-Out” and similar covering agents are expressly
forbidden.
1
The values that you record on your data sheet must have:
Units (such as kg for kilograms)
Reasonable uncertainty estimates for given instru ments and procedures
Precision co nsistent with uncertainty (proper significa nt digits)
Propagation of error for calculated quantities
Your lab instructor’s initials.
If you happen to forget your lab manual, then you will take your data on notebook paper.
Your lab instructor will initial that as your data sheet and you will turn that in with your lab
report as well as your own data sheet from the lab manual.
You may not use your lab
partner’s datashe et and then make a photocopy.
IV. Graphs: You must follow the guidelines in the lab manual for all graphs. The first graphs of
the semester must be made by hand, not computer software. After your lab instructor gives
permission, you may use computer software to make graphs. Those graphs must also
conform to the guidelines in the lab manual. Remember that when plotting data with units,
both the slope and intercept of a graph also have uni ts.
V. Sample Calculations: Show calculations in a neat and orderly outline form. Include a brief
description of the calculation, the equation, numbers from your data substituted into the
equation and the result.
Do not include the intermediate steps. Numbers in the sample
calculations must agree with what you recorded in your data sheet. For calculations
repeated many times, you only include one sample calculation. Answers should have the
proper number of significant figures and units. (It is not necessary to show the calculation for
obtaining an average, unless your TA reque sts that you do so.)
Typing the equation into the lab report is not required; it is easier and faster to print these
calculations neatly by hand. If you wish to type this section, then use the equation editor in
Microsoft Word. Your lab instructor can give you information on using the equ ation editor.
VI. Discussion of Results: This is the most important part of the lab report; it is where you
analyze the data. (In the future, you may not actually collect data; a lab technician or other
people may collect the raw data. Regardless of your discipline, the most challenging and
rewarding part of your work will be analy zing the data.)
Begin the discussion with the experimental purpose and briefly summarize the basic idea of
the experiment with emphasis on the measurements you made and transition to discussing
the results. State only the key results (with uncertainty and units) quantitatively with numerical
values; do not provide intermediate quantities. Your discussion should address questions
such as:
What is the relationship between your measurements and your final results?
What trends were ob servable?
What can you conclud e from the graphs that you made?
How did the independent variables affect the dependent variable s? (For example,
did an increase in a given measured (indepe ndent) variable re sult in an increase or
decrease in the associated calculated (dependent) variable?)
Then describe how
your experimental results substantiate/agree with the theory. (This is not
a single statement that your results agree or disagree with theory.) When comparison values
are available, discuss the agreement using either uncertainty and/or percent differences.
This leads int o the discussion of the sources of error.
In your discussion of sources of error, you should discuss all those things that affect your
measurement, but which you can't do anything about given the time and equipment
constraints of this laboratory. Included in this would be a description of sources of error in
your measurement that bias your result (e.g. friction in pulleys that are assumed frictionless in
2
the formula). Your analysis should describe the qualitative effect of each source of error (e.g.
friction slowed motion, causing a smaller value of acceleration to be measured) and, where
possible, provide an estimate of the magnitude of the errors they could induce. Describe
only the prominent sources of error in the experiment. For example, the precision of the triple
balance beam, a fraction of a gram, compared to the 250.0 g lab cart is not significant. Note
that a tabulation of all possible errors without any discussion of qualitative effect of the error
will receive no credit. Your discussion should address question s such a s:
Are the deviations due to error/uncertain t y in the experimental meth od, or are they due to
idealizations inherent in the theory (or both)?
If the deviations are due to experimental uncertainties, can you think of ways to d ecrease
the amount of unce rtainty?
If the deviations are due to idealizations in the theory, what factors has the theory
neglected to consider? In either case, consider whether your results display systematic
or random deviations.
A conclusion is not required in the rubric. You will not lose points for leaving this out.
However, in order to receive the points for a very well written report in Achievements and
Flaws, a
brief conclusion i s recommended.
Considerations: These are not questions to be answered as a separate part of the lab report.
They are hints. They are things for you to think about. Some of them should be addres sed in
your lab report. Not becau se your TA says to do so, but because it adds depth to your
discussi on. You are nev er to simply list answers to considerations.
Endnotes:
The report should not be a big production. It should not take hours to write. The objective is to
write down the significant details of the experiment, the analysis of the experimental data. A few
neatly written pages, including your data sheets will suffice for most experiments. Hopefully the
sample lab report that follows will help you.
Note:
1. No student should copy data from anyone who is not his or her lab partner.
2. You may discuss the experiment with your lab partner and other classmates, but the lab
report that you turn in must be your own work. Lab reports are subj ect to all the rules
governing ac ademic honesty.
3. Photocopies of any parts o f the lab report are not permissible.
3
Hooke’s Law Experiment
Objective: To measure the spring constant of a spring using two different methods.
Background: If a weight, W = mg, is hung from one end of an ordinary spring, causing
it to stretch a distance x, then an equal and opposite force, F, is created in the spring
which opposes the pull of the weight. If W is not so large as to permanently distort the
spring, then this force, F, will restore the spring to its original length after the load is
removed. The magnitude of this restoring force is directly proportional to the stretch,
F = -kx
The constant k is called the spring constant. To emphasize that x refers to the change in
length of the spring we write
F = mg = - k ∆
l (1)
In this form it is apparent that if a plot of F as a function of ∆
l has a linear portion, this
provides confirmation that the spring follows Hooke's Law and enables us to find k.
An additional approach is possible. One definition of simple harmonic motion is that it is
motion under a linear, “Hooke's Law” restoring force. Note that for simple harmonic
motion, the period does not depend upon the amplitude of the oscillation. For such a
motion, we have
22
4/Tm
π
= k
(2)
where k again is the spring constant, T is the period of the pendulum and m is the mass that
is oscillating. Thus, the mass includes the mass of the spring itself. However, the entire
spring does not vibrate with the same amplitude as the load (the attached mass) and
therefore it is reasonable to assume that the effective load (m) is the mass hung from the
end of the spring plus some fraction of the mass of the spring. Based on similar
experiments, one third of the mass of the spring is a good estimation of the effective load
due to the spring, thus
1
3
load es load spring
mm m m m=+=+
where m
es
is the effective load of the spring. Using this in Eq. (2), we find
2
2
4{ 1/3( )}
load spring
mm
k
T
π
+
=
(3)
The effective load of the spring can be determined for a particular spring using the following
process. The equation for T
2
can be written in terms of m
load
and m
es
; m
es
can then be
determined from a graph of T
2
versus m
load
. Note that this assumes that m
es
is constant.
4
Eq (3) uses an approximation for the contribution of the mass of the spring to the
oscillation. If we rewrite Eq (2) as the effective mass of the spring and hanging mass
(load), then
22
22
ES
load ES load
44
T4m m k m
kk
ππ
=π + = +()/
m
(4)
where m
load
is the hanging mass and m
ES
is the effective mass of the spring. If we assume
that the effective spring mass is the same for all loads, then a graph of period squared (T
2
)
vs. hanging mass (m
load
) is a straight line, where 4π
2
/k is the slope and 4π
2
m
ES
/k is the
intercept.
Procedure:
Part 1
Meter StickMeter Stick
1. Hang a spring from a horizontal metal rod.
2. Attach a mass hanger directly to the bottom of the hanging
spring and record the position of the bottom of the mass
hanger relative to a meter stick.
3. Add masses to the spring and record the position of the bottom
of the mass hanger.
Part 2
1. Hang a mass from the spring and use a stopwatch to time 15
oscillations of the mass and spring.
2. Repeat for other masses.
5
Assemble report using a
staple in the upper left corner.
Physics 1408 Section A1
HOOKE’S LAW AND A SIMPLE SPRING
Your Name
Partner(s): Full Name(s)
Date Performed: October 21, 2005
TA: Full Name
Abstract
Two experiments were performed to find the spring constant of a steel spring. The spring
constant was determined statically, by measuring its elongation when subjected to
loading, and dynamically, by measuring the period of a mass hung from one end and set
into vertical oscillation. The resulting values of 2.94 ± 0.01 N/m and 2.98 ± 0.02 N/m,
respectively. Our spring's behavior followed Hooke's law to within the limits of accuracy
of the two experiments. (76 words)
An Alternate Abstract:
The purpose of this experiment was to measure and compare the spring constant of a steel
spring using two different procedures. First we investigated the relationship between the
force applied to a spring and the displacement of the spring from its rest length. We
hung various masses from the springs, and measured the vertical displacement. We found
a spring constant of 2.94 ± 0.01 N/m. Our results confirmed Hooke’s Law, F
s
= -kx. In
the second procedure, we set the spring into vertical oscillation with a suspended mass
and measured the period of oscillation. Using this method, we found a spring constant of
2.98 ± 0.02 N/m. Our results verified that the period of oscillation depended on the
effective mass of the spring and the period of oscillation. (128 words)
A lab report
should include a
title page like this
one, with all of the
appropriate
in
f
ormation.
6
A Poor Abstract – Too long because it has too much detail and unnecessary
information. (The worst problems are in italics.)
The purpose of this experiment was to determine the spring constant k of a steel spring
using two different methods. First we investigated the relationship between the force
applied to a spring and the displacement of the spring from its rest length in order to
verify Hooke’s law. We hung masses of 0.01 kg, 0.20 kg, 0.30 kg, 0.04 kg, 0.05 kg, 0.06
kg, 0.70 kg, and 0.80 kg from the springs, and recorded the vertical displacements. We
made four measurements for each mass hung from the spring and used the average of the
four values in order to reduce random error. In this method, the main cause of error was
measurement. We found a spring constant of k = 2.94 ± 0.01 N/m. Our results confirmed
Hooke’s Law, the well known relationship that the magnitude of an elastic restoring
force on a spring is directly proportional to the displacement of the spring.
This
relationship is named after the 17th century scientist Hooke who studied it. Next we
measured the period of a mass hung from one end of a spring and set into vertical
oscillation. We performed this process using the four different masses 0.145 kg, 0.105
kg, 0.055 kg, and 0.025kg. The period of each mass was measured three times using
three different amplitudes of oscillation. We found that the spring constant depended on
the effective mass of the spring and the period of oscillation. The period of the motion
was the same whether the amplitude of the oscillation is large or small. In this method,
the main cause of error was reaction time. Using this method we found a spring constant
of 2.98 ± 0.02 N/m. This value is consistent with the result obtained using the first
method. (291 words)
Remember to be concise.
7
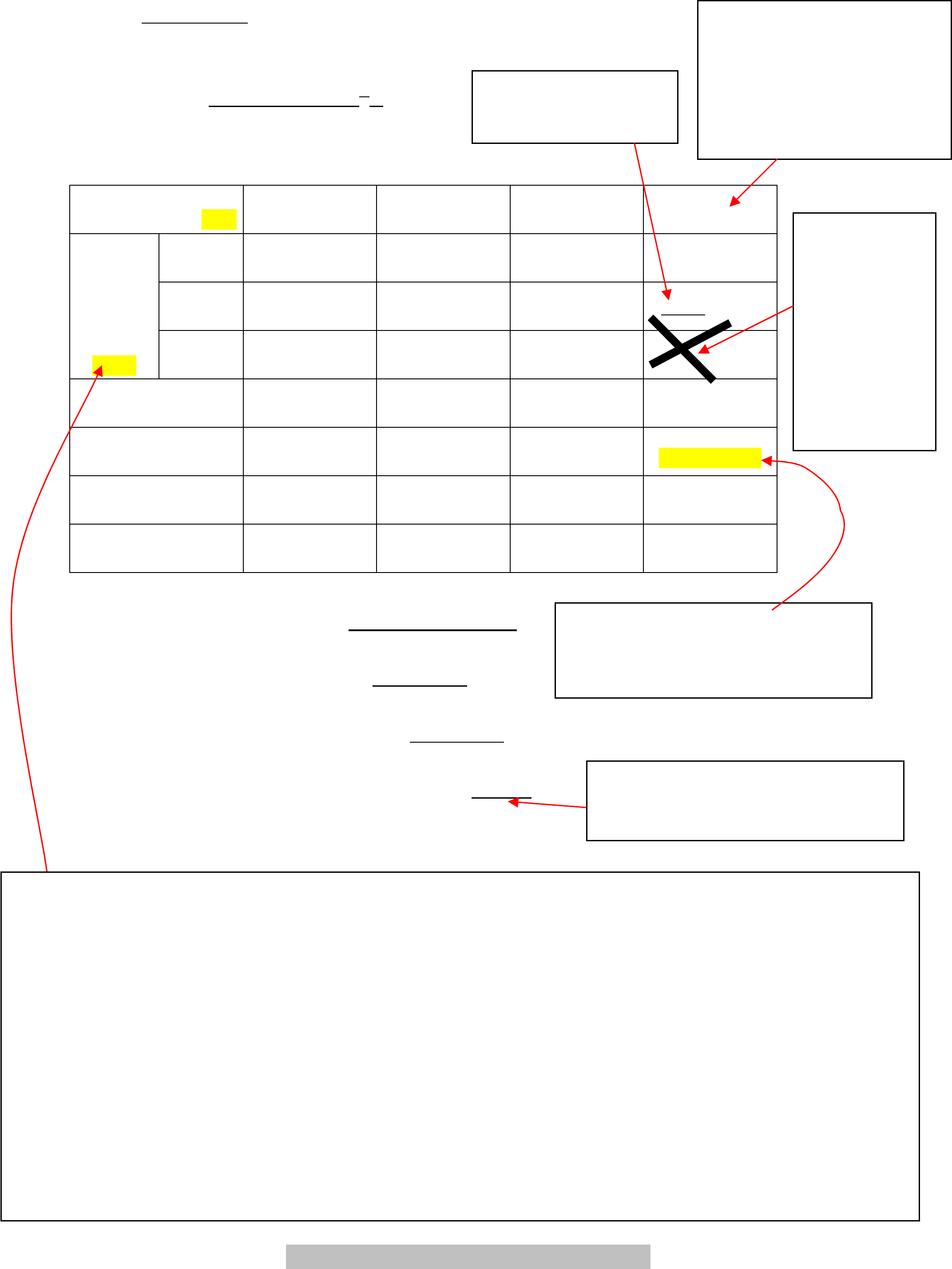
Name: ___
_Your Name________ Date:__Date Exp. Performed
Partner: ___Partners Full Name__
Hooke’s Law and a Simple Spring
Part 1
Table 1
Location of the Mass Hanger Reference in cm ±0.05cm
Position
Mass
( g )
±1%
Trial 1
Trial2
Trial 3
Trial 4
Reference
0 69.55 69.50 69.50
69.50
1
1 69.27 69.19 69.18 69.17
2 3 68.61 68.50 68.53 68.52
3 5 67.95 67.87 67.88 67.86
4
10 66.42 66.20 66.21 66.20
5
20 62.90 62.89 62.90 62.93
6
40 56.32 56.22 56.30 56.23
7
60 49.65 49.60 49.61
49.6
8
80 42.97 42.97 42.95 42.95
9
100 36.32 36.30 36.32 36.32
10 120 29.63 29.70 29.72 29.72
11 140 23.07 23.05 23.10 23.12
Table 2
Force Displacement ( x10
-2
m )
( N )
Trial 1 Trial 2 Trial 3 Trial 4 Average
±1% ±0.07 ±0.07 ±0.07 ±0.07
Spring
Constant
(N/m )
0.00981
-0.28 -0.36 -0.37 -0.38 -0.35 ± 0.02 2.8 ± 0.2
0.0294 -0.94 -1.05 -1.02 -1.03 -1.01± 0.02 2.91± 0.08
0.0491 -1.60 -1.68 -1.67 -1.69 -1.66± 0.02 2.96± 0.05
0.0981 -3.13 -3.35 -3.34 -3.35 -3.29± 0.05 2.98± 0.05
0.196 -6.65 -6.66 -6.65 -6.62 -6.65± 0.01 2.95± 0.03
0.392 -13.23 -13.33 -13.25 -13.32 -13.28± 0.02 2.95± 0.03
0.589 -19.90 -19.95 -19.94 -19.95 -19.94± 0.01 2.95± 0.03
0.785 -26.58 -26.58 -26.60 -26.60 -26.59± 0.01 2.95± 0.03
0.981 -33.23 -33.25 -33.23 -33.23 -33.24± 0.01 2.95± 0.03
1.18 -39.92 -39.85 -39.83 -39.83 -39.86± 0.02 2.95± 0.03
1.37 -46.48 -46.50 -46.45 -46.43 -46.47± 0.02 2.96± 0.03
Average Spring Constant k = __2.94 ± 0.01 N/m _
Spring Constant k from Graph = __ 2.95 N/m ________
TA’s Initials on data sheet
If the value
is four sig
figs then
include the
trailing 0.
If you drop
that zero
then it is 3
sig figs!
This should
have been
49.60!
You can
include
uncertainty
for a tool
such as a
meter stick
in the top
of a data
table.
Uncertainty
can be
written as a
percentage.
For the
subtraction
all the
uncertainties
were the
same; thus it
was put in
the top of a
column; that
was not
possible for
the average.
Do you
know why
there are
only 2 sig
figs here?
Calculate the standard error.
There is a way to find the uncertainty for slopes of
g
ra
p
hs
,
but we will not do that in this course.
Remember to include units and uncertainty.
8
Name: ___
_Your Name________
Part 2:
Mass of spring =
10.19 ± 0.02 x 10
-3
kg____
Table 3
Load (x10
-3
kg)
(mass of spri ng) ±1%
145 105 55.0
25.0
Trial 1
(small)
27.94 23.98 17.60 12.32
Trial 2
(medium)
27.79 24.06 17.44
12.56 12.40
Time for
20
oscillations
(s)
±0.08
Trial 3
(large)
27.90 23.95 17.34 12.03 12.34
Average
20 oscillations (s)
27.88 ± 0.04 24.00± 0.03 17.46± 0.08 12.35± 0.02
Period (s)
1.394± 0.002 1.200± 0.002 0.873± 0.004
0.618± 0.001
Period
2
(s
2
)
1.943 ± 0.006 1.440 ± 0.004 0.762± 0.007 0.382 ± 0.00 1
k from Eq. (3) (N/m)
3.01 ± 0.03 2.97± 0.03 3.02± 0.04 2.94± 0.03
Average Spring Constant k = __ 2.98± 0.02 N/m_
Spring Constant k from Graph = __ 3.01 N/m_
Spring’s Effective Mass from Graph = _
_0.0040 kg
% Difference between k in Part 1 and Part 2 =
_ 2 %_
Cross out mistakes
with a single line; do
not use white
-
out.
Do not cross
out mistakes
this way!
Sometimes
what you had
was correct.
You may
want to be
able to read
it.
Period was 12.35s/20= 0.6175s
Uncertainty was 0.001; thus we
write the period with 3 sig figs
(
0.618
)
k in parts 1 and 2 was 3 sig figs;
but the difference between the
two values is one sig fig!!!!
With 1% uncertainty in
the slotted masses, the
uncertainty for 145g is
±1g and for 55g, it is
±0.06g; thus for the
smallest two loads, can be
written in the form below.
Remember to include an uncertainty!
Guessing and then seeing what the value is for the average of a small number of trials helps build your ability to
predict uncertainty.
Why 0.08 in this case? One way to measure your reaction time is to have a friend hold a meter stick vertically
between your thumb and first finger; note the cm mark between your fingers; the friend drops the meter stick, and
you catch it. Determine how far it fell before your caught it. Since it had no initial velocity and the only force
acting on the meter stick is gravity, then d=½gt
2
. For most people, the distance the meter stick falls is about 15 cm.
However, there is a difference between someone dropping a meter stick and timing an oscillating object. When
timing an object, we can observe the motion and use the rhythm to reduce reaction time error. This might reduce
the timing error to a third of the original value: t
reaction time
/3 = sqrt(2d/g)/3 = 0.06 s
However, there are two uncertainties – starting the stopwatch and stopping the stopwatch; thus, we need to
propagate the error. ∆t = sqrt(∆t
start
+ ∆t
start
) = ∆t
reaction time
sqrt(2) = 0.08s
We might have made a different assumption, then we might have used had a value or 0.05 to 1.0 s.
Remember to include units and uncertainty
9
10
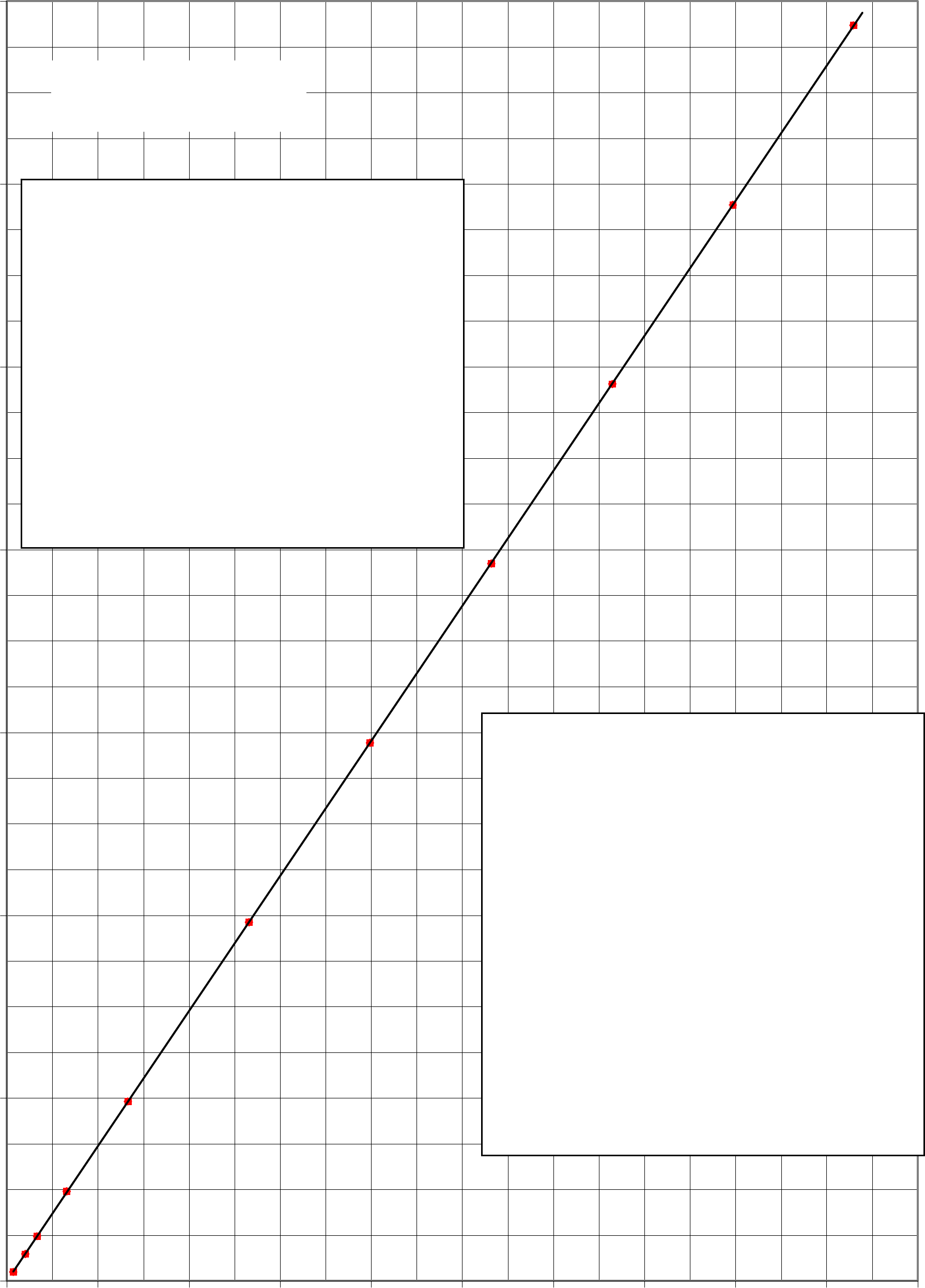
Restoring Force vs. Displacement Magnitude
Force = 2.95x - 0.0001
x = displacemn t
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50
Displacement Magnitude (m)
Force (N)
Not all graphs will start at zero as this
one does. If your data range for the y-
axis is from 6 to 20 newtons, then use a
graph that starts at 5 and ends on 20 or 25
newtons.
Never force a line to go through the
origin. NEVER!!
Your TA may have other information
that he/she wants on a graph. Then be
sure to include that.
Graphs must conform to all the rules
given in lab handbook.
Each graph should be on a separate page.
This graph was inserted into this Word
document by a simple “copy and paste”
from Excel into Word.
Note that for the first one or two
experiments each semester you will be
required to make your graphs by hand.
After you demonstrate an ability to make
a graph by hand, then you may use
computer software to make your graphs.
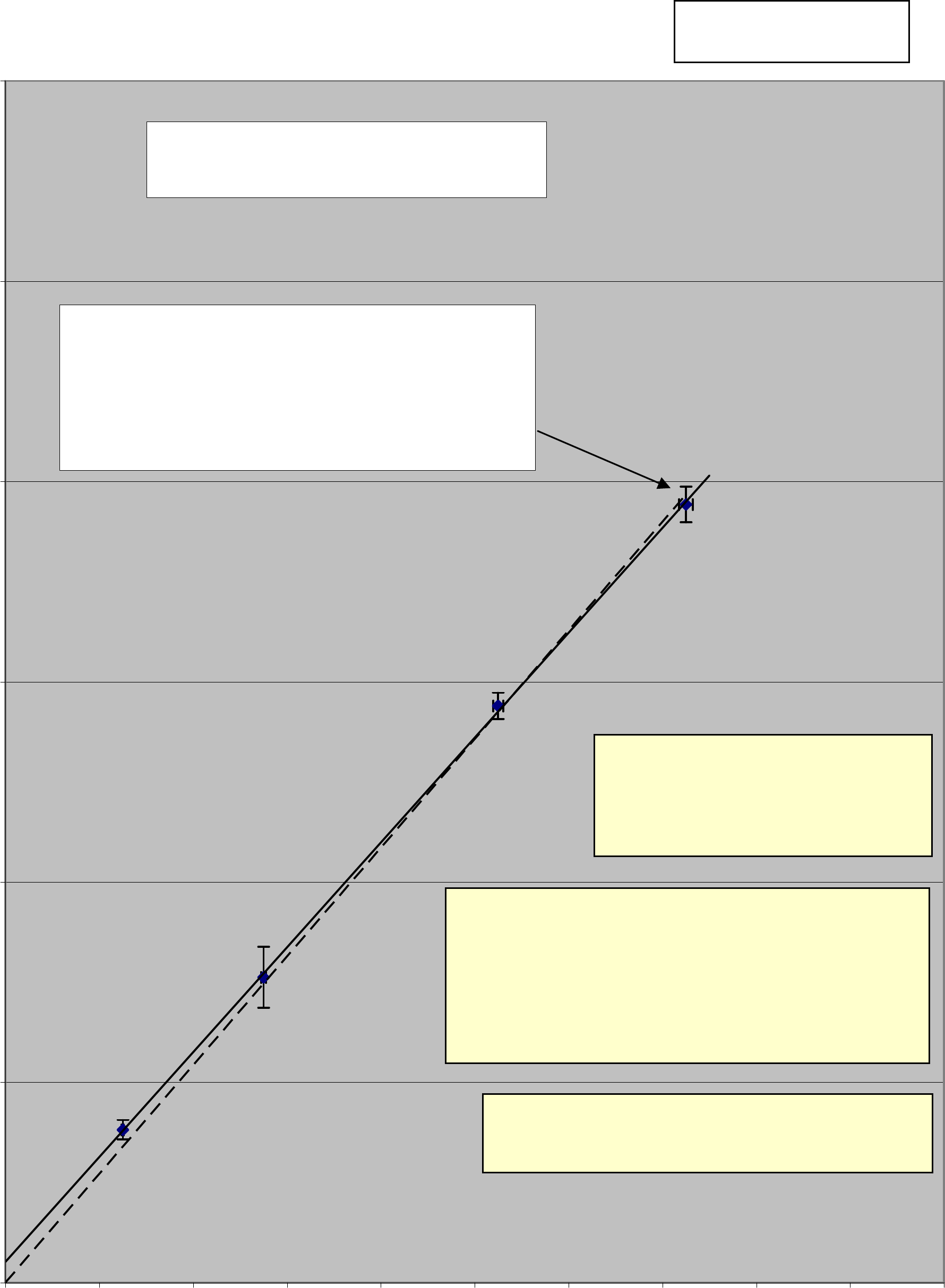
Mass vs. Time Squared
y = 13.09x + 0.052
If you use E xcel then edit x and y so it looks lik e t his
T
2
= 13.09M +.052
y = 13.566x
Dashed curve forced to intercept the origin
0
0.5
1
1.5
2
2.5
3
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
Mass
Time
2
Do not force a curve!
Error bars were added to this graph to show that
when the curve was forced to go through the origin
it then did not honor the data collected.
This title is incorrect!
Do you know why?
Do not use the default backgound
color, use white. It can be difficult
to see data points when printed.
A
dd gridlines for both axes, not just the default as
in this plot.
Scale the graph so that the data is spread across
the graph. This graph has too much unused
space.
Since there are two graphs - each is worth 5
points. I would give this graph only 2 points out
of 5.
11
