Fillable Printable HP 12C Loan Amortizations
Fillable Printable HP 12C Loan Amortizations

HP 12C Loan Amortizations

hp calculators
HP 12C Loan Amortizations
Amortization
The HP12C amortization approach
Practice amortizing loans
hp calculators
HP 12C Loan Amortizations
hp calculators - 2 - HP 12C Loan Amortizations - Version 1.0
Amortization
The word 'amortization' comes from a Latin word meaning "about to die". When a loan earning interest has regular, fixed
payments, it is said that the loan is being paid off or amortized. Although the debt is reduced by the same periodic
payments, different parts of each payment are applied against the principal and against the interest. The interest is
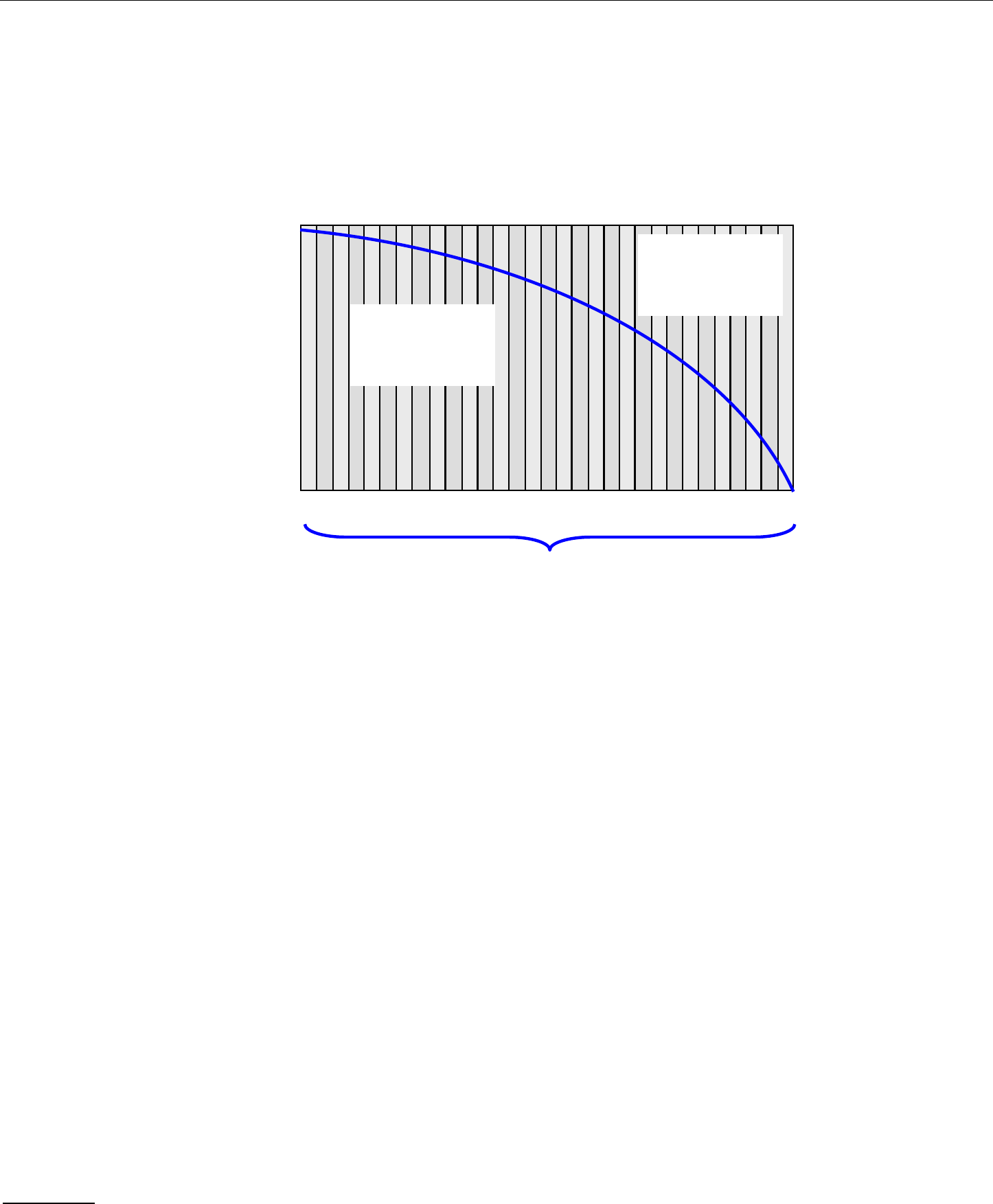
deduced from each payment and the remaining amount is used to reduce the debt. Figure 1 illustrates this process.
Figure 1
The HP12C amortization approach
In the HP12C, amortization uses the contents of the following Time Value of Money (TVM) registers:
n - used as a reference and contains the number of payments amortized
¼ - periodic interest rate
P - periodic payment
$ - remaining balance
The display must contain the number of payments to be amortized before executing f!. It is important to keep in
mind that on the HP12C, amortization is a sequenced calculation. This means that once a number of payments is
amortized, all subsequent balances refer to the next amortized payments. If it is necessary to go back and review
previous balance, some values must be restored to their default values. This is because every time f! is pressed,
the following registers have their contents updated:
$ - contents updated to remaining balance
n - contents updated to current number of payments amortized
The following examples illustrate the HP12C amortization approach.
Practice amortizing loans
Example 1: Calculate the first year of the annual amortization schedule for a 30-year, $180,000 mortgage at 7.75%,
compounded monthly.
1 2 3 . . . . . . . . . . . . . . . . . . . n
Number of
p
a
y
ments
Periodic Payment
(fixed value)
Part of each
payment related
to interest
Part of each
payment related
to the principal

hp calculators
HP 12C Loan Amortizations
hp calculators - 3 - HP 12C Loan Amortizations - Version 1.0
Solution: Clear the TVM registers contents to zero and set END mode:
fG gÂ
Set the relevant TVM values and calculate the PMT:
7.75 gC 30 gA 180000 $ 0 M P
Figure 2
To calculate the first year it is necessary to set n to zero and amortize twelve payments:
0 n 12 f!
Figure 3
This is the total interest paid after one year. To see the part of the principal that is paid, press:
~
Figure 4
To check the loan balance after one year:
:$
Figure 5
Answer: After one year, the loan balance is $178,420.18. The amount of principal paid so far is $1,579.82 and
$13,894.66 interest has been paid.
Example 2: With all data from the previous example still available in the calculator's memory, calculate the second year
of the annual amortization of the same mortgage.
Solution: Just to make sure the calculator is at the proper point in the loan, recall the contents of n to the display:
:n
Figure 6

hp calculators
HP 12C Loan Amortizations
hp calculators - 4 - HP 12C Loan Amortizations - Version 1.0
Now it is necessary to input the number of payments to be amortized. In this example, twelve more
payments must be amortized to calculate the second year:
12 f!
Figure 7
This is the total interest paid after two years. To see the part of the principal that is paid, press:
~
Figure 8
To check the loan balance after one year, press:
:$
Figure 9
Answer: After two years, the loan balance is $176,713.49. The amount of principal repaid is $1,706.69 and the
amount of interest paid is $13,767.79.
Example 3: Amortize the 10
th
payment of a 4-year car loan. The loan amount is $12,500 and the interest rate is 10.2%,
compounded monthly. Assume monthly payments starting immediately.
Solution: Clear the TVM registers contents to zero and set BEGIN mode:
fG g×
Set the relevant TVM values and calculate PMT:
10.2 gC 4 gA 12500 $ 0 M P
Figure 10
To amortize the 10
th
payment it is necessary to amortize the first nine payments and then amortize the 10
th
separately:
0 n 9 f! 1 f!
hp calculators
HP 12C Loan Amortizations
hp calculators - 5 - HP 12C Loan Amortizations - Version 1.0
Figure 11
This is the interest paid with the 10
th
payment. To see the part of the principal that is paid:
~
Figure 12
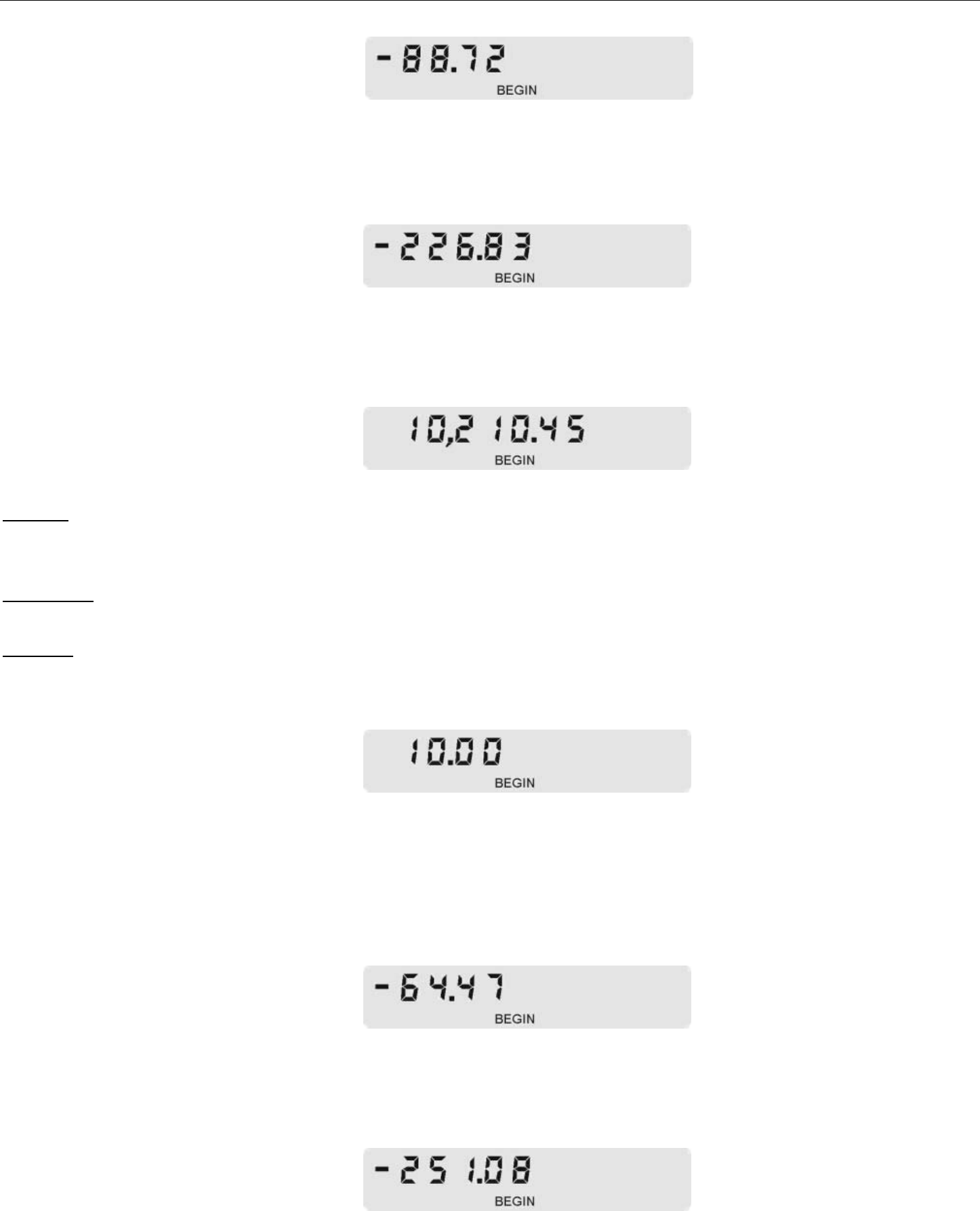
To check the loan balance after ten payments:
:$
Figure 13
Answer: After ten payments, the loan balance is $10,210.45. With the 10
th
payment, the amount of principal that has
been paid is $226.83 and $88.72 interest has been paid.
Example 4: With all data from the previous example still available in the calculator memory, amortize the 22
nd
payment.
Solution: Just to verify the calculator is still in the proper state, recall the contents of n to the display:
:n
Figure 14
To amortize the 22
nd
payment it is necessary to amortize the next eleven payments and then amortize the
22
nd
separately:
11 f! 1 f!
Figure 15
This is the interest paid with the 22
nd
payment. To see the part of the principal that is paid:
~
Figure 16

hp calculators
HP 12C Loan Amortizations
hp calculators - 6 - HP 12C Loan Amortizations - Version 1.0
To check the loan balance after ten payments, press:
:$
Figure 17
Answer: After twenty-two payments, the loan balance is $7,333.27. With the 22
nd
payment, the amount paid toward
principal is $251.08 and $64.47 interest has been paid.